Estructures de dades

Segons Niklaus Wirth (i altres autors) un programa és:

programa = algorismes + estructures de dades

En aquest apartat veurem les formes mes estàndard d'organitzar les dades i proposarem alguns exercicis en Python.

És important aclarir que parlarem de TADs o Tipus Abstractes de Dades. Aquests es defineixen per uns elements contenidors de les dades i unes operacions sobre aquestes. La implementació que se'n pugui fer d'aquestes pot utilitzar eines molt diverses. Per exemple, el TAD stack té les operacions push() i pop() i sempre s'utilitzarà igual, però podem tenir implementacions realitzades amb vectors o amb llistes enllaçades, cadascuna d'aquestes implementacions amb els seus avantatges i inconvenients.

Tipus bàsics que no analitzarem

No poso apunts sobre aquests perquè ja els hem anat veient al llarg del curs, però sempre està bé fer un esment. Per aprofundir podeu llegir l'article d'estructures de dades a la Viquipèdia (aquest cop en català).

• Vector: arranjament d'elements contigus als que accedim per indexació.
  • Avantatges: accés més ràpid
  • Desavantatges: estructura estàtica (tamany fix).
• Matriu: vectors de 2 o més dimensions. De vegades es parla de vector i matriu indistintament.
• Llista: conjunt d'elements dispersos als que es pot accedir seqüencialment.
  • Avantatges: estructura dinàmica (podem afegir, esborrar i insertar elements més eficientment).
  • Desavantatges: accés més lent (seqüencial).

Cua

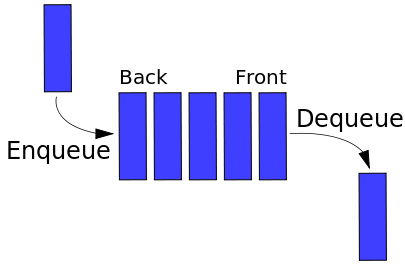
Una cua (enllaç Wikipedia) és una estructura de dades de tipus FIFO: First In First Out. Té dos extrems (front i back). Les operacions permeses son:

• encuar(e): insertar l'element "e" al final (back) de la cua.
• desencuar(): extreure element del principi (front) de la cua.

No es pot insertar en posicions intermitges ni es poden extreure elements del mig. Les operacions, doncs, estan limitades a aquestes dues. Podem afegir una funció auxiliar que resulta útil:

• esbuida(): retorna True si està buida i False si hi ha algun element.

Exemple en Python

Suposant que tenim la class Cua() implementada (ja veieu que us tocarà a vosaltres fer-la ;P ), s'utilitzaria d'aquesta manera:

class Cua(object):
   ...
>>> c = Cua()
>>> c.encua(10)         # c = [10]
>>> c.encua(23)         # c = [10,23]
>>> c.encua(79)         # c = [10,23,79]
>>> num = c.desencua()  # num = 10 ; c = [23,79]
>>> print num           # comportament FIFO: ha sortit el primer d'entrar (10)
10

Pila o stack

Una pila (enllaç Wikipedia) és una estructura de dades de tipus LIFO: Last In First Out. Té un sol extrem: el top. Les operacions permeses s'efectuen sempre en el "top" i son:

• push(e): inserta l'element "e" a la pila.
• pop(): llegir i extreure l'element del top.
• peek(): llegir (sense extreure) l'element del top.

No es pot insertar ni extreure en posicions intermitges ni per cap altre extrem que no sigui el "top". També podem definir la funció auxiliar:

• esbuida(): retorna True si la pila està buida i False si hi ha algun element a dins.

Exemple en Python

Suposant que tenim la class Pila() implementada (ja veieu que també us tocarà a vosaltres fer-la ;P ), s'utilitzaria d'aquesta manera:

class Pila(object):
   ...
>>> p = Pila()
>>> p.push(10)       # c = [10]
>>> p.push(23)       # c = [10,23]
>>> p.push(79)       # c = [10,23,79]
>>> num = p.pop()    # num = 79 ; c = [10,23]
>>> print num        # comportamet LIFO: ha sortit l'últim d'entrar (79)
79

Aplicacions típiques de la pila:

• Resolució d'operacions matemàtiques algebraiques.
• Mecanismes d'aniuament com els contexts d'execució d'una CPU.
  • Segur que tots heu consultat alguna dia la web Stack Overflow: http://stackoverflow.com . Aviam si algú sap explicar de què va aquest nom.
• Algorismes de backtracking (exploració de totes les possibilitats de resolució d'un problema). El típic sol ser el de cercar la sortida d'un laberint.
• Aquí trobareu alguns exemples d'aplicacions de piles dels que hem comentat, en particular el del laberint i el de resolució d'operacions algebraiques.

Arbres

...

Diccionaris o hash tables

...

Exercicis

1- Implementacions en Python

Implementeu les classes Cua() i Pila() derivant-les de la classe list nativa de Python. La classe list ja disposa de mètodes que poden equivaldre al de les estructures cua i pila, però volem que tinguin els noms dels mètodes tal i com estan en el TAD.

• Cua: mètodes encua(elem), desencua() i esbuida()
• Pila: mètodes push(elem), pop(), peek() i esbuida()

Per saber més mireu les descripcions dels mètodes fetes més amunt.

2- Comprovador d'expressions matemàtiques algebraiques

Utilitzeu les classes Cua() i Pila() definides en l'anterior exercici per resoldre un comprovador d'expressions matemàtiques.

Un exemple d'expressió algebraica correcta seria:

25+3*(1+2+(30*4))/2

Exemples erronis:

25+3*(1+2+(30*4))/(2
25+3*(1+2+(30*4))/)2(
25+3*(1+2)+(30*4))/2

Com que realitzar el càlcul d'una expressió algebraica és complicat, limitarem l'exercici a comprovar que els parèntesis siguin correctes.

L'algorisme ha de fer:

1. Extreure els parèntesis de l'expressió i ficar-los en la Cua. En l'exemple (bo) de més amunt ens quedarien els següents elements a la cua:

   ['(','(',')',')']

2. Extreure element per element de la Cua i avaluar-lo utilitant la Pila:
   • Si és "(" el fiquem a la pila.
   • Si és ")" extraiem un element de la pila. Si és un "(" tot ok. Si hem esgotat la pila, és que hi ha un error.
3. Al final de l'algorisme la pila ha d'estar buida, altrament és que hi ha algun error.

3- Avaluador d'expressions matemàtiques

Farem una versió simplificada d'un avaluador d'expressions matemàtiques. Aplicarem certes restriccions per facilitar l'aplicació.

Restriccions (constraints):

• A l'expressió només hi pot haver:
  • Nombres sencers positius: 1, 10, 215, etc.
  • Parèntesis: ( i )
  • Operadors: + - / *
• Les operacions s'han de fer obligatòriament en grups de 2 operands. No podem fer 2+10+12, per exemple. Si volem fer això caldrà fer (2+10)+12
• S'han de posar parèntesis explícits per avaluar l'expressió (en grups de dos).

Exemples correctes:

(3+5)
(6+((1+12)/2))
(((18+3)*2)+4)

Exemples incorrectes:

3+5      => (3+5)
(6+3/2)  => ((6+3)/2)

Amb aquestes restriccions serà més fàcil fer l'aplicació de resolució d'expressions matemàtiques.

Tokenitzador

Abans que res caldrà tokenitzar l'expressió que ens ve en un string. Un "token" és un element significatiu per l'aplicació, com un número, un operador o un parèntesi.

Cal fer una funció tokenitza(s) que ens transformarà l'expressió en elements lògics: un string són caràcters sense significat; en canvi, després de "tokenitzar" tindrem elements significatius amb els què operar:

Exemple: abans de tokenitzar:

(6+((1+12)/2))

Després de tokenitzar, tindrem els següents elements (en una llista).

( , 6 , + , ( , ( , 1 , + , 12 , ) , / , 2 , ) , )

La dificultat està en extreure els nombres. Els altres elements són molt fàcils perquè son d'un sol caràcter (parèntesis i operands).

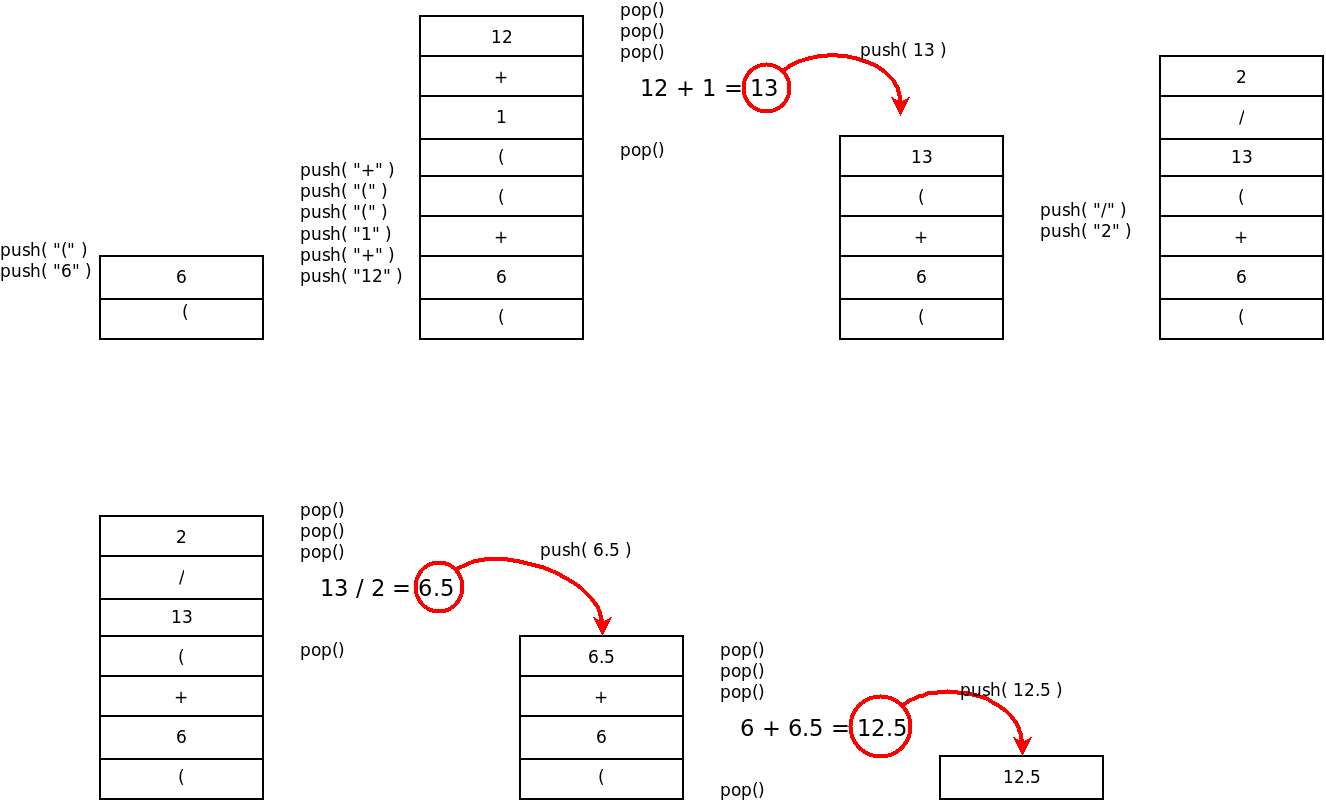
Algorisme simplificat

Penseu que aquest algorisme de resolució d'expressions és una versió simplificada per les expressions que hem descrit anteriorment.

1. Entrar expressió
2. Tokenitzar-la i introduïr-la a l'objecte Cua()
3. Avaluar l'expressió amb l'ajuda de l'objecte Pila(). Anem tibant els elements de la cua i...
   1. Si és qualsevol cosa menys un ")" ho posem a la pila.
   2. Si és un ")" avaluem els 3 darrers elements (número + operador + número)
   3. Extraiem el "(" de la pila (si no hi és, és que hi ha error)
   4. Col·loquem el resultat a la pila

Al final el resultat ha d'estar disponible a la pila.

4- Laberint (Maze)

Resoldrem la sortida d'un laberint amb 2 algorismes diferents: recursiu i amb pila (stack).

Contindrem el laberint en una matriu. Indica a cadascuna de les cel·les si té:

• * = mur
• . = espai buit
• I = Inici (només pot haver 1)
• F = Final (només pot haver 1)

S'entén que no es pot sortir de la matriu (ens envolta un mur) i que cal començar per la cel·la d'inici (I) i resoldrem el joc quan arribem al final (F).

El programa ha de poder:

1. Generar un laberint (matriu) a partir d'un fitxer de text. Podeu agafar el del final per provar, però genereu-ne vosaltres més. Convindria que chequejés que té 1 sol inici (I) i un sol final (F).
2. Mostrar laberint.
3. Trobar la sortida del laberint. Ha retornar una llista amb les posicions a recórrer des del inici (I) fins el final (F).
4. Mostrar laberint + camí de sortida.
5. Sortir

Podeu agafar aquest exemple per començar el laberint:

I*....
.*.***
...*..
..*...
....*.
**.*.F

És el mateix que en aquesta web, però invertit perquè quadrin les files: http://www.laurentluce.com/posts/solving-mazes-using-python-simple-recursivity-and-a-search/

Llegeix també l'article sobre Algorisme de backtracking a cacauet.org

IMPORTANT PER ENTREGAR:

• Implementar el programa en un objecte Laberint com s'indica a Algorisme de backtracking.
• Afegir les funcionalitats que demana l'exercici (menú)
• Implementar un mètode soluciona(nom_fitxer) que busqui la cel·la d'inici i retorni una llista amb la solució fins la sortida.